Статья Дугласа Заре
2001 год

Я профессиональный математик и эксперт по нардам (мой ник на GridGammon, FIBS и GameSite2000 - zare).  В этой колонке я хочу обсудить теоретические аспекты игры в нарды, но не ради их  самих. Лучшее понимание теории игры, может помочь играть лучше, и лучше понимать саму игру. Я никогда не буду рекомендовать вам делать сложные арифметические вычисления за столом. Я так же не буду требовать от вас знаний высшей математики, и не буду требовать от вас, что бы вы умели делать сложные расчёты, для того, что бы понимать эту колонку. Я пишу для обыкновенных парней, игроков в нарды, не математиков.

Рассмотрим цену гаммона. Мы рассмотрим стандартное определение стоимости гаммона, как вы можете использовать стоимость гаммона, и почему стандартное определение ошибочно.

Стоимость гаммона это полезная идея. Стоимость гаммона подскажет вам, какую ценность имеет гаммон, при различных значениях куба. Вы, конечно, сможете выбрать, играть ли вам на гаммон, или побеждать в одиночных играх.  В одних случаях ход очевиден, так как он дает больше шансов выиграть гаммон, но в других случаях, иногда, приходиться рисковать некоторыми шансами на  победу, что бы получить больше шансов на гаммон. Стоимость гаммона предполагает, сколькими шансами на победу вы можете пожертвовать, чтобы выиграть гаммон.

Стандартное определение стоимости гаммона.  
Предположим, что игрок выигрывает игру без гаммона в 100% случаев, а другой в 90% случаев, включая 15% победы гаммоном. Какой вариант игры вы должны выбрать в манигейме? Что, если вы отстающий 3-1 в 5-и очковом матче, а куб уже удвоен? Стандартное определение стоимости гаммона, это разница между выгодой, когда вы побеждаете с гаммоном и  простой (single) победой, поделенная на разницу между простой победой и простым поражением.

Стоимость гаммона = (победа гаммоном-простая победа)/(простая победа-простое поражение)

Для манигейма, если куб повернут на 2, и вы побеждаете гаммоном, то вы выигрываете 4 очка. Когда вы одерживаете простую победу, и куб повернут на 2, то  выигрываете 2 очка, и когда вы проигрываете простую игру, то вы проигрываете 2 очка.

Таким образом, стоимость гаммона в нашем случае:

                         
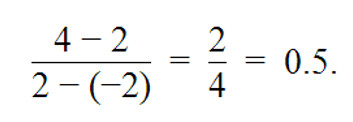
Это говорит о том, чтобы получить дополнительно 15% побед гаммоном, вы должны быть готовы отдать всего: 15% * 0,5 = 7,5% побед. Вы должны играть безопасно.
Отставание 1-3 в матче до 5-ти:
Если вы побеждаете с гаммоном, то побеждаете в матче (100% вероятность победы в матче, или «ВПМ»).
Если вы одерживаете простую победу, то счет в матче становится 3-3. Это по таблице матчевого эквити 50% ВПМ.
Если вы проигрываете, то проигрываете в матче (0% ВПМ).
Таким образом, стоимость гаммона получается:

                       
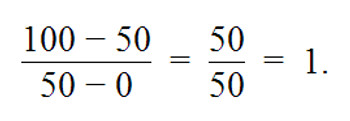
Чтобы получить дополнительно 15% побед гаммоном, вы должны быть готовы отдать всего: 15% * 1 = 15% побед. Вы должны играть на гаммон.
Стоимость гаммона в матче до 7, согласно SNOWIE.

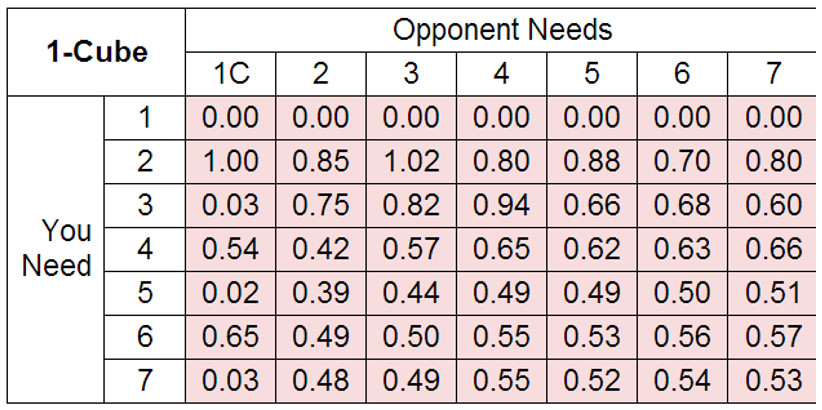
Здесь первая колонка, это игра с правилом Кроуфорда. Нам не нужна победа с гаммоном, если для победы в матче необходимо одно очко. Победа гаммоном ценна в случае, если вам до победы не хватает четного количества очков, и вы предполагаете, что сразу удвоите в следующей игре. И гаммон не особо ценен, если до победы не хватает нечетного количества очков. Я не запомню эту таблицу, но стоит отметить, что при кубе равном 1, часто бывает, что цена гаммона выше для лидера, нежели для отстающего игрока, в случае, когда лидеру необходимо 2, 3 или 4 очка до победы. В начале матча, стоимость гаммона примерно равна стоимости гаммона в манигейме. Хорошо знать об исключительных счетах в матчах, таких, например, как 3-away/4-away, и иметь, хотя бы общее представление об других счетах.

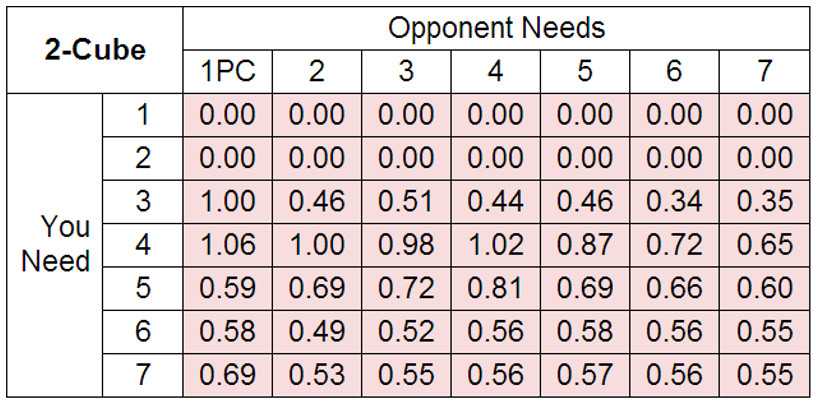
Здесь первая колонка, значения после Кроуфорда. В остальной части таблицы особенно важно, когда один игрок решает, стоит ли удваивать. По всей видимости, стоимость гаммона в манигейме и в матче, примерно одинакова, если вам необходимо 3 очка до победы (за исключением пост-Кроуфорда).  Если вам необходимо 4 очка, то стоимость гаммона значительно выше в матче, чем в манигеймах. Вообще, при удвоенном кубе, стоимость гаммона даже в начале матча до 7-ми, немного выше, чем в манигейме. При отставании 2-away/4-away, стоимость гаммона очень велика, в случае, когда одному игроку не хватает до победы 2 очка, а другому максимальное значение, то стоимость гаммона, в этом случае, не отличается от стоимости гаммона в манигейме.

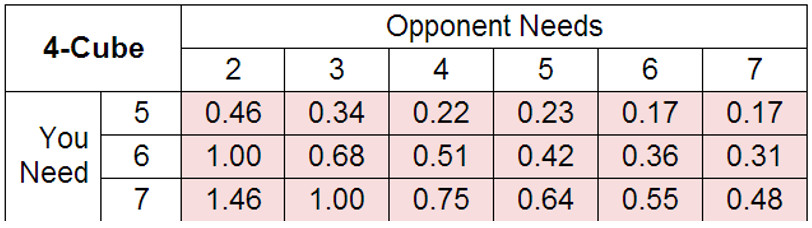
Здесь не должно быть, при значении куба равном 4, пост Кроуфорда. Когда до победы в матче не хватает 4 или меньше очков, стоимость гаммона равняется нулю. Стоимость гаммона велика, когда вы, выиграв 4 очка, не станете сильным фаворитом, и, напротив, если вы, проиграв 4 очка, станете отстающим, то стоимость гаммона не велика. В качестве примера того, как можно использовать стоимость гаммона при игре в матче, давайте предположим, что вы лидируете со счетом 3 – 1 в матче до 5-и очков. Вам необходимы 2 очка, в то время, как вашему сопернику нужно 4 очка для победы в матче. Ваш соперник предлагает удвоение куба. Для вас, стоимость гаммона при кубе равном 2-м, равна нулю. Если вы принимаете удвоение куба, то гаммон для вас не имеет значение. Напротив, для вашего соперника, стоимость гаммона равна 1. Ценность гаммона очень велика для вашего соперника, и очень разрушительна для вас. Таким образом, если вы предполагаете, что у вашего соперника вероятность победы 65%, включая 20% побед гаммоном, 65% + 1*20% = 85%, то вы должны пасовать.

Это является альтернативой запоминанию таблицы матчевого эквити с точностью до 3-х знаков и выполнению действий с ними: Вместо этого, вы можете запомнить точки тейка и стоимости гаммона. Позиция, с подобными статистическими данными в манигейме  могла бы стать уверенным тейком и отказом от удваивания, но при этом счете в матче, это пас. Даже если вы не можете получить точные цифры к позиции, вы можете быть осторожней в получении двойного гаммона, если цена гаммона будет высока после тейка. 

Применение к позиции
Позиция, которая рассматривается в этой статье, находится в завершающей стадии. Стоимость гаммона применима гораздо раньше, но если мы можем рассмотреть победу гаммоном или проигрыш гаммоном, то это сильно упрощает задачу.
В этой позиции черные отстают в гонке 135 – 72 и должны играть 52.

 
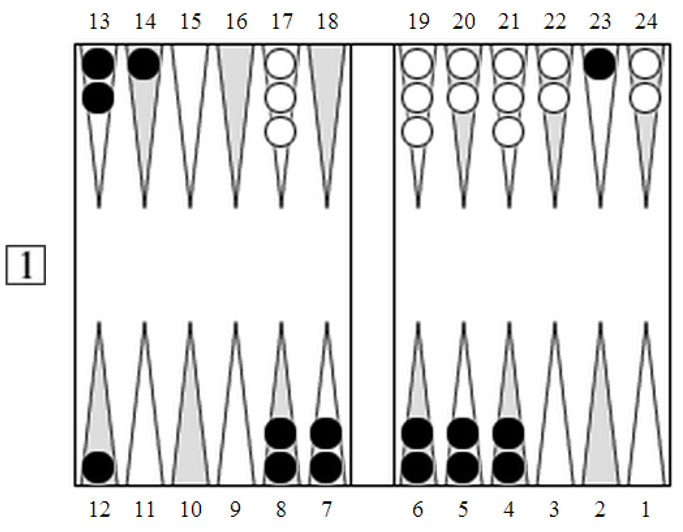
Черные безнадежно отстали в гонке. Естественная альтернатива 23/16, это почти гарантированный проигрыш, но этот ход позволит сэкономить на гаммоне, или остаться с риском получить гаммон, и сыграть 13/11, 14/9 и сохранить надежду впоследствии получить шот надежды. Мы можем спросить у Snowie, что она считает правильной игрой. Оценки Snowie хороши, но не так, как ее ролауты. Есть определенные трудности, как делать ролауты и каким результатам верить, но это мы обсудим в другой статье, а сейчас, давайте предположим, что данные ролаута точны для любых счетов в матче.

Это значит, что вы не можете выиграть гаммон и бэкгаммон, а ваши шансы на простую победу составляют 0,3%, и что, вы проиграете в 99,7% случаев, включая 6,4% гаммонов.

После 14/9, 13/11 ролл аут показывает, что вы выиграете в 11% случаях, включая 0,8% выигрыш гаммоном, или, что вы проиграете в 89% случаях, включая 41,5 % проигрыша гаммоном, а так же 0.1% проигрыш бэкгаммон.

Вот различие вариантов игры:

Игнорируя выигрыши гаммоном и проигрыши бэкгаммон, эффект от отказа от побега это проигрыш дополнительно 35% гаммоном, что бы выиграть 10,7% игр. Это имеет смысл, только в том случае, если стоимость гаммона вашего оппонента не выше, чем 10,7/35 = 0,31.

Предположим, что куб равен 2. Тогда согласно второй таблице, показанной выше, вы должны убегать при счете в матче, где имеет значение гаммон, так как все записи, по крайней мере, 0,34. Вполне вероятно, что отставание 3-away 6-away и 3-away 7-away, было бы исключением, если бы вы владели кубом. Если куб равен 4, то тогда вы можете остаться только тогда, когда проигрыш гаммона имеет значение, при счете n-away/5-away, где n равен 4, и, возможно, 7-away 6-away. В случае манигейма, вы должны убегать.

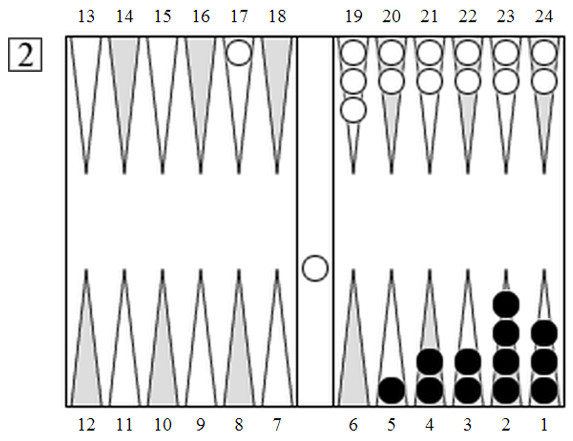
В этой позиции, где черные должны сыграть 11, вы можете сыграть осторожно 5/2, 1/off, или попытаться получить немного больше гамонов, сыграв 5/4, 1/off, 2/off. Ролаут на Snowie показывает, что последний ход дает дополнительно 5,1% вероятности гамона, но уменьшает вероятность победы на 3,6%. Таким образом, ход 5/2, 1/off уместен, в том случае, когда стоимость гамона меньше 3,6/5,1= 0,71. В случае мани гейма, вы должны играть осторожно, т.е. первый ход. Если в матче вы отстаете 4-away/3-away, то должны играть на гаммон. Предположим, что в этой позиции счет в матче 4-away/5-away. Должны ли вы играть на гаммон? Лидируете вы или отстаете, при стоимости гаммона 0,8, вы должны играть на гамон, не так ли? Не обязательно! Существует проблема со стандартным определением стоимости гаммона в случае, когда куб может быть использован (когда куб не мертв), и эта проблема просматривается даже в манигеймах.

Эквити без учета куба и стоимость гаммона в манигейме
Эквити без учета куба в позиции:
-3 х проигрыш backgammon
-2 х проигрыш гаммоном
-1 х одиночный проигрыш
+1 х одиночная победа
+2 х победа гаммоном
+3 х победа backgammon

Эквити без учета куба часто используется, но что в реальной игре важней, это эквити с учетом куба. Некоторые люди говорят, что эквити без учета куба 0,550 , представляет собой пограничный пас. Если ли способ преобразовать эквити без учета куба в эквити с учетом куба, так что эквити без учета куба 0,550 соответствовали эквити с учетом куба 1,0? Нет. Там есть способ преобразования в эквити с учетом куба оценочных значений побед или поражений, одиночных, гаммоном и коксом.